Problem:
Implement Inorder Traversal of a binary tree without using recursion, and print the elements. Use an iterative approach (do not use recursive function calls).
Note: If you want preorder traversal without recursion. Click here.
If you want postorder traversal without recursion. Click here.
My Approach:
First, let us understand what inorder traversal is.
Inorder traversal of a binary tree means visiting nodes in the following order:
1. Left subtree
2. Root node
3. Right subtree
If we are using recursion, then we can perform this traversal by using the following code snippet:
inorder(node) {
if(node == null) return;
inorder(node.left);
print(node.data);
inorder(node.right);
}
But, we should follow iterative approach instead of this recursion. So, I will use stack data structure here.
The following are the steps for inorder traversal using stack:
1. Initialize a stack and set node = root.
2. Now, repeat the following until the stack is empty and node is null.
- Go to the leftmost node. It means, while node is not null, push node onto the stack and set node as node.left.
- Now pop the node from the stack and print its data.
- Now set node as node.right.
It's because, inorder traversal follows (left - root - right). By pushing all left nodes onto the stack first ensures that the leftmost node is processed before its parent. The stack keeps track of the nodes we need to return to after finishing the left subtree. Once we pop a node from the stack, we process it (print its data) and then move to its right child. This makes sure that we correcty follows (left - root - right) order.
- For large trees, we may get stack overflow if we use recursion. But iteration helps us in that case.
- At the same time, it is easy to implement using simple push and pop operations.
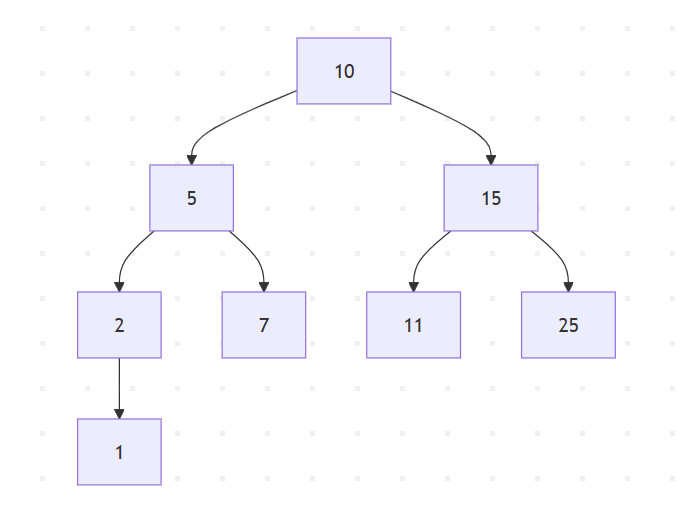
Let us consider a binary tree
For the above binary tree, the inorder traversal is given as
1 - 2 - 5 - 7 - 10 - 11 - 15 - 25
Lets do step by step process to solve.
Step 1:
Initialize the stack and set node as root.
node = 10
Stack = [ ]
Step 2:
As node is not null, push node 10 onto the stack and then set node as node.left
node = 5
Stack = [10]
Step 3:
As node is not null, push node 5 onto the stack and then set node as node.left
node = 2
Stack = [10, 5]
Step 4:
As node is not null, push node 2 onto the stack and then set node as node.left
node = 1
Stack = [10, 5, 2]
Step 5:
Push node 1 onto the stack and set node as node.left
node = null
Stack = [10, 5, 2, 1]
Step 6:
Now node is null. So pop the top node "1" from the stack and print it. And now set node as right child of popped node "1".
node = null
Stack = [10, 5, 2]
Output = 1 -
Step 7:
Now node is null. So pop the top node "2" from the stack and print it. And now set the node as right child of the popped node "2".
node = null
Stack = [10, 5]
Output = 1 - 2 -
Step 8:
Node is null. So, pop the top node "5" from the stack and print it. And now set the node as right child of popped node "5"
node = 7
Stack = [10]
Output = 1 - 2 - 5 -
Step 9:
Node is not null. So push the node 7 onto the stack and set node and node.left
node = null
Stack = [10, 7]
Output = 1 - 2 - 5 -
Step 10:
Node is null. So, pop the top node "7" from the stack and print it. And set the node as right child of popped node "7".
node = null
Stack = [10]
Output = 1 - 2 - 5 - 7 -
Step 11:
Node is null. So, pop the top node "10" from the stack and print it. And set the node as right child of popped node "10".
node = 15
Stack = [ ]
Output = 1 - 2 - 5 - 7 - 10 -
Step 12:
Node is not null. So, push the node 15 onto the stack and set node and node.left
node = 11
Stack = [15]
Output = 1 - 2 - 5 - 7 - 10 -
Step 13:
Node is not null. So, push the node 11 onto the stack and set node and node.left
node = null
Stack = [15, 11]
Output = 1 - 2 - 5 - 7 - 10 -
Step 14:
Node is null. So, pop the top node "11" from the stack and print it. And set the node as right child of popped node "11".
node = null
Stack = [15]
Output = 1 - 2 - 5 - 7 - 10 - 11 -
Step 15:
Node is null. So, pop the top node "15" from the stack and print it. And set the node as right child of popped node "15".
node = 25
Stack = [ ]
Output = 1 - 2 - 5 - 7 - 10 - 11 - 15 -
Step 16:
Node is not null. So, push the node 25 onto the stack and set node and node.left
node = null
Stack = [25]
Output = 1 - 2 - 5 - 7 - 10 - 11 - 15 -
Step 17:
Node is null. So, pop the top node "25" from the stack and print it. And set the node as right child of popped node "25".
node = null
Stack = [ ]
Output = 1 - 2 - 5 - 7 - 10 - 11 - 15 - 25 -
Step 18:
Now, node is null and stack is empty. So, our traversal ends here.
Now let us get into the codes. I will provide you JS and Python codes.
JS Code:
// Tree Node class
class Node {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
}
// Stack class
class Stack {
constructor() {
this.stack = [];
this.top = -1;
}
push(node) {
this.top++;
this.stack[this.top] = node;
}
pop() {
if(this.top === -1) return null;
let node = this.stack[this.top];
this.top--;
return node;
}
isEmpty() {
return this.top === -1;
}
}
// Iterative Inorder Traversal using Stack
function inorderTraversal(root) {
if (!root) {
console.log("Tree is empty");
return;
}
let stack = new Stack();
let node = root;
while (node || !stack.isEmpty()) {
// Reach the leftmost node of the current node
while (node) {
stack.push(node);
node = node.left;
}
// Node with no left child
node = stack.pop();
process.stdout.write(`${node.data} - `) // Print the node value
// Visit the right subtree
node = node.right;
}
}
// Create the tree
const root = new Node(10);
root.left = new Node(5);
root.right = new Node(15);
root.left.left = new Node(2);
root.left.left.left = new Node(1);
root.left.right = new Node(7);
root.right.left = new Node(11);
root.right.right = new Node(25);
inorderTraversal(root);
This is the inorder traversal of a binary tree without using recursion. I used a stack to visit the nodes in the order: left - root - right.
Which approach do you like more iterative or recursive? Comment below!
If you have any doubts, comment below!
Comments
Post a Comment