Binary Tree Postorder Traversal Without Recursion

Problem:

Implement Postorder Traversal of a binary tree without using recursion, and print the elements. Use an iterative approach (do not use recursive function calls). 

Note: If you want inorder traversal without recursion. Click here.

           If you want preorder traversal without recursion. Click here.

My Approach:

First, let us understand what postorder traversal is.

Postorder traversal of a binary tree means visiting nodes in the following order:

1. Left subtree

2. Right subtree

3. Root node

If we are using recursion, then we can perform this traversal by using the following code snippet:

postorder(node) {

    if(node == null) return;

    postorder(node.left);

    postorder(node.right);

    print(node.data);

}

But since recursion is not allowed, we should follow iterative approach. So, I will use stack data structure here.

The following are the steps for postorder traversal using stack:

1. Initialize two stacks such as temp_stack and final_stack.

2. Push the root node into the temp_stack.

3. Now, repeat the following until the temp_stack is empty.

• Pop the top node from the temp_stack.
• Push this node into final_stack.
• Push its left child into temp_stack only if it exists.
• Similarly, push its right child into temp_stack only if it exists.

4. After this process, the final_stack contains nodes in Root -> Right -> Left order.

5. Now, pop all nodes from final_stack and print them. This gives Left -> Right -> Root order.

Actually we have good advantage by doing iteration instead of recursion. 

• For large trees, we may get stack overflow if we use recursion. But iteration helps us in that case.
• At the same time, it is easy to implement using simple push and pop operations.

Time Complexity : O(n), where n is the number of nodes. Each node is pushed and popped exactly once from the first stack, and again once from the second stack. That’s still linear, so total = O(n).

Space Complexity : O(n), since in the worst case both stacks together can hold all n nodes.

Now let us do example break-through.

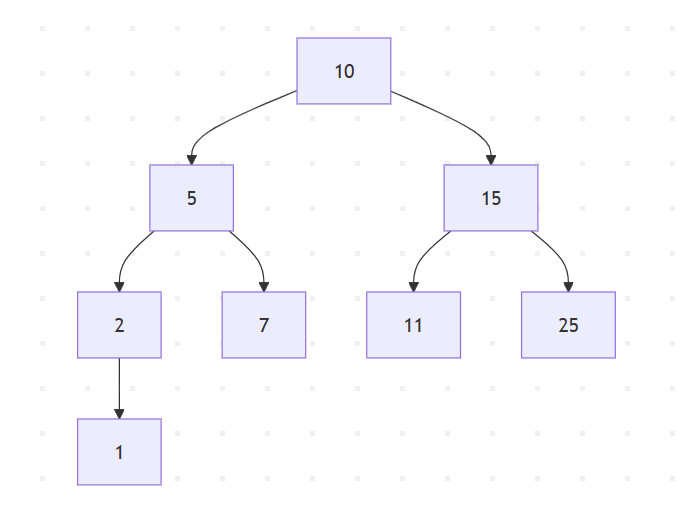
Let us consider a binary tree 

For the above binary tree, the postorder traversal is given as 

1 - 2 - 7 - 5 - 11 - 25 - 15 - 10

Lets do step by step process to solve.

Step 1: 

Initialize both the stacks temp_stack and final_stack  and push the root node into temp_stack

temp_stack = [10 ]

final_stack = [ ]

Step 2:

Now pop the top node from the temp_stack ( node 10 ) and then push it onto the final_stack. At the same time, push the popped node's (10) left and right child onto the temp_stack.

temp_stack = [5, 15]

final_stack = [ 10]

Step 3:

Pop the top node from the temp_stack ( node 15 ) and then push it onto the final_stack. At the same time, push the popped node's (15) left and right child onto the temp_stack.

temp_stack = [5, 11, 25]

final_stack = [ 10, 15]

Step 4:

Pop the top node from the temp_stack ( node 25 ) and then push it onto the final_stack. Node 25 don't have any left child or right child. So, go to next step.

temp_stack = [5, 11]

final_stack = [ 10, 15, 25]

Step 5:

Pop the top node from the temp_stack ( node 11 ) and then push it onto the final_stack. Node 11 don't have any left child or right child. So, go to next step.

temp_stack = [5]

final_stack = [ 10, 15, 25, 11]

Step 6:

Pop the top node from the temp_stack ( node 5 ) and then push it onto the final_stack. At the same time, push the popped node's (5) left and right child onto the temp_stack.

temp_stack = [2, 7]

final_stack = [ 10, 15, 25, 11, 5]

Step 7:

Pop the top node from the temp_stack ( node 7 ) and then push it onto the final_stack. Node 7 don't have any left child or right child. So, go to next step.

temp_stack = [2]

final_stack = [ 10, 15, 25, 11, 5, 7]

Step 8:

Pop the top node from the temp_stack ( node 2 ) and then push it onto the final_stack. At the same time, push the popped node's (2) left and right child onto the temp_stack. Here node 2 only has left child. So push it.

temp_stack = [1]

final_stack = [ 10, 15, 25, 11, 5, 7, 2]

Step 9: 

Pop the top node from the temp_stack ( node 1 ) and then push it onto the final_stack. Node 1 don't have any left child or right child. So, go to next step.

temp_stack = []

final_stack = [ 10, 15, 25, 11, 5, 7, 2, 1]

Step 10:

Now the temp_stack is empty. So start popping from the final_stack and print the values.

Output : 1 - 2 - 7 - 5 - 11 - 25 - 15 - 10

Now let us get into the codes. I will provide you JS and Python codes.

JS Code:

// Tree Node class

class Node {

    constructor(data) {

        this.data = data;

        this.left = null;

        this.right = null;

    }

}

// Stack class

class Stack {

    constructor() {

        this.stack = [];

        this.top = -1;

    }

    push(node) {

        this.top++;

        this.stack[this.top] = node;

    }

    pop() {

        if (this.top === -1) return null;

        let node = this.stack[this.top];

        this.top--;

        return node;

    }

    isEmpty() {

        return this.top === -1;

    }

}

// Iterative Postorder Traversal using Two Stacks

function postorderTraversal(root) {

    if (!root) {

        console.log("Tree is empty");

        return;

    }

    let temp_stack = new Stack();

    let final_stack = new Stack();

    temp_stack.push(root);

    while (!temp_stack.isEmpty()) {

        let node = temp_stack.pop();

        final_stack.push(node);

        if (node.left) temp_stack.push(node.left);

        if (node.right) temp_stack.push(node.right);

    }

    while (!final_stack.isEmpty()) {

        process.stdout.write(`${final_stack.pop().data} - `);

    }

}

// Create the tree

const root = new Node(10);

root.left = new Node(5);

root.right = new Node(15);

root.left.left = new Node(2);

root.left.left.left = new Node(1);

root.left.right = new Node(7);

root.right.left = new Node(11);

root.right.right = new Node(25);

postorderTraversal(root);

Output: 1 - 2 - 7 - 5 - 11 - 25 - 15 - 10 -

Python Code:

# Binary Tree Node

class Node:

    def __init__(self, data):

        self.data = data

        self.left = None

        self.right = None

# Iterative Postorder Traversal using Two Stacks

def postorderTraversal(root):

    if not root:

        print("Tree is empty")

        return

    temp_stack = []

    final_stack = []

    temp_stack.append(root)

    while temp_stack:

        node = temp_stack.pop()

        final_stack.append(node)

        if node.left:

            temp_stack.append(node.left)

        if node.right:

            temp_stack.append(node.right)

    while final_stack:

        print(final_stack.pop().data, end=" - ")

# Sample Binary Tree

root = Node(10)

root.left = Node(5)

root.right = Node(15)

root.left.left = Node(2)

root.left.left.left = Node(1)

root.left.right = Node(7)

root.right.left = Node(11)

root.right.right = Node(25)

postorderTraversal(root)

Output: 1 - 2 - 7 - 5 - 11 - 25 - 15 - 10 -

Conclusion:

This is the postorder traversal of a binary tree without using recursion. I used a two stack implementation.

Which approach do you like more iterative or recursive? Comment below!

If you have any doubts, comment below!