Iterative Preorder Traversal of a Binary Tree - No Recursion

Problem:

Implement a Preorder Traversal of a binary tree without using recursion, and print the elements.

• Use an iterative approach (do not use recursive function calls).

• Do not store elements in a linked list or array; just print the elements in preorder order.

Note: If you want Inorder traversal without recursion. Click here.

My Approach:

First let us understand what is preorder traversal.

Preorder traversal of a binary tree means visiting nodes in the following order:

1. Root node (Access it or Print it)

2. Left subtree

3. Right subtree

If we are using recursion, then it is very easy to do. The following code snippet shows how it works : 

preorder(node) {

        if(node == null) return;

        print(node.data);

        preorder(node.left)

        preorder(node.right)

}

But in our problem, we should not use recursion. We should use iterative approach for this.

So, I'm using stack data structure here.

Okay! Now I will say how a stack helps us to perform preorder traversal.

1. First initialize a stack and push the root node into the stack.
2. Now until the stack is not empty, do the following :

• Pop the top node from the stack.
• Print its data
• Push its right child onto the stack if it exists.
• Push the left child onto the stack if it exists.

Here you may have doubt like why are we pushing the right child first and then the left child.

Its because, stack follows LIFO (Last In First Out). So when we push the right child first and then the left child, the left child will be in top position. So when we do pop operation, we can get the left child first before the right child. So, it helps us to maintain the preorder property ( root - left - right ).

And, we have good advantage also by doing iteration instead of recursion. 

• For large trees, we may get stack overflow if we use recursion. But iteration helps us in that case.
• At the same time, it is easy to implement using simple push and pop operations.

Time Complexity : O(n), where n is the number of nodes. Each node is visited exactly once.

Space Complexity : O(h), where h is the height of the tree.

Now let us do example break-through.

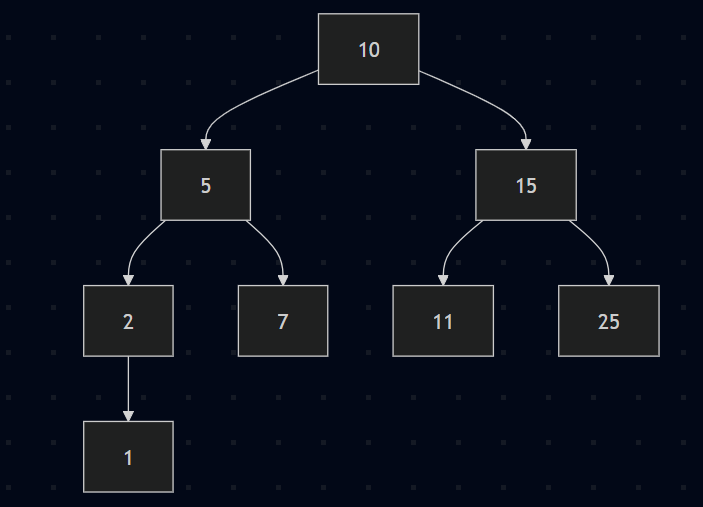
Let us consider a binary tree 

For the above binary tree, the pre order traversal is given as 

10 - 5 - 2 - 1 - 7 - 15 - 11 - 25

Lets do step by step process to solve.

Step 1: 

Initialize the stack and push the root node (10) onto the stack.

Stack: [10]

Step 2: 

Pop 10 and print 10. Now push right child first (15) of node 10 onto the stack, then left child (5).

Stack: [15, 5]

Output: 10 -

Step 3: 

Pop 5 and print 5. Now push right child (7) of node 5 onto the stack, then left child (2).

Stack: [15, 7, 2]
Output: 10 - 5 - 

Step 4: 

Pop 2 and print 2. Now push right child (none) of node 2 onto the stack, then left child (1).

Stack: [15, 7, 1]
Output: 10 - 5 - 2 - 

Step 5: 

Pop 1 and print 1. Here node 1 has no children. So, nothing is pushed.

Stack: [15, 7]
Output: 10 - 5 - 2 - 1 -

Step 6: 

Pop 7 and print 7. Here node 7 has no children. So, nothing to push.

Stack: [15]
Output: 10 - 5 - 2 - 1 - 7 - 

Step 7: 

Pop 15 and print 15. Now push right child (25) of node 15 onto the stack, then left child (11).

Stack: [25, 11]
Output: 10 - 5 - 2 - 1 - 7 - 15 - 

Step 8: 

Pop 11 and print 11. Here 11 has no children. So, nothing to push.

Stack: [25]
Output: 10 - 5 - 2 - 1 - 7 - 15 - 11 - 

Step 9: 

Pop 25 and print 25. Here 25 has no children. So, nothing to push.

Stack: [ ] empty
Output: 10 - 5 - 2 - 1 - 7 - 15 - 11 - 25 -

Now let us get into the codes. I will provide you JS and Python codes.

JS Code:

// Binary Tree Node

class Node {

    constructor(data) {

        this.data = data;

        this.left = null;

        this.right = null;

    }

}

// Stack class

class Stack {

    constructor() {

        this.stack = [];

        this.top = -1;

    }

    push(data) {

        this.top++;

        this.stack[this.top] = data;

    }

    pop() {

        if(this.top == -1) return null;

        let data= this.stack[this.top];

        this.top--;

        return data;

    }

    isEmpty() {

        return this.top == -1;

    }

}

// Preorder traversal function  

function preorderTraversal(root) {

    if(!root) {

        console.log("Tree is empty");

        return;

    }

    let stack = new Stack();

    stack.push(root);

    while(!stack.isEmpty()) {

        let node = stack.pop();

        process.stdout.write(`${node.data} - `); // Print the node data

        if(node.right)

            stack.push(node.right);

        if(node.left)

            stack.push(node.left);

    }

}

// Sample Binary Tree

let root = new Node(10);

root.left = new Node(5);

root.right = new Node(15);

root.left.left = new Node(2);

root.left.right = new Node(7);

root.right.left = new Node(11);

root.right.right = new Node(25);

root.left.left.left = new Node(1);

preorderTraversal(root);

Output: 10 - 5 - 2 - 1 - 7 - 15 - 11 - 25 -

Python Code:

# Binary Tree Node

class Node:

    def __init__(self, data):

        self.data = data

        self.left = None

        self.right = None

# Preorder traversal function 

def preorderTraversal(root):

    if not root:

        print("Tree is empty")

        return

    stack = []

    stack.append(root)

    while stack:

        node = stack.pop()

        print(node.data, end=" - ")  # Print node data

        # Push right first, then left

        if node.right:

            stack.append(node.right)

        if node.left:

            stack.append(node.left)

# Sample Binary Tree

root = Node(10)

root.left = Node(5)

root.right = Node(15)

root.left.left = Node(2)

root.left.right = Node(7)

root.right.left = Node(11)

root.right.right = Node(25)

root.left.left.left = Node(1)

preorderTraversal(root)

Output: 10 - 5 - 2 - 1 - 7 - 15 - 11 - 25 -

Conclusion

This is the preorder traversal of a binary tree without using recursion. I used a stack to visit the nodes in the order: root - left - right.

Key Points:

• Push the right child first, then the left child so the left node is accessed first before the right.
• Using a stack avoids stack overflow, which can happen with recursion in large trees.
• Each node is visited once, so the time complexity is O(n) and space complexity depends on the tree height O(h).
• Works for any binary tree and can be done in JavaScript, Python, C++, or Java. It works in C too, but we have to implement the stack ourself.

This method is simple, safe for large trees, and easy to understand.

Which approach do you like more - iterative or recursive? Comment your thoughts.

If you have any doubts, comment below!